あ、あ、あ。
文を読むということはとてもむつかしい。下手に漢字をひらいても読みにくいし、修飾子と非修飾語を離したり、句点を、こんなふうに、やられるのは、とても、よみにくい。難解な漢字もなく、たとえ音読をできたとしても、そこに何が書かれているかの文意をくみ取ることは、目が滑るばかりで、なにより、よほどむつかしい。３割の日本人は日本語が読めないなどとひとはいふが、読みにくく書かれたものはことさらにむつかしい。

３割と書いたが、そもそも割り算はむつかしいものだ。分数でふるい落とされる小３を９歳の壁といったりするそうだが、割り算の概念は足し算や引き算、掛け算と脳の使う場所が違うのだとかなんだとか。老人ホームなんかでも割り算が先にだめになるなんてのをどっかで読んだような聞いたような。ケーキを等分できない人たちがいるそうだけど、むべかるかな。割り算に必要な抽象化ができないと、計算はできるが割り算がわからない。割り算がわからないと並び替えができない。並び替えができなければ優先順位付けやリソースの分配はできない。

さて、さて。
ちゅう事で、掲題からもわかるとおり、ちょいと障害がらみのセンシティブなところに踏み込んだ内容になりそうだったので、無駄なまくら文章を書いてみた。４行以上の文は基本読まれないし、グラフや幾何的な情報から情報を浚うことはむつかしいので多分大丈夫。

そんなわけで、正規分布のお話し。

これは平成３１年の小学校６年生男子の身長の分布図。
こういう真ん中にもっとも厚みがくる分布は正規分布、ベル型（ベル曲線）と言われたりするもっとも典型的な分布だ。いろんなものを、適当な評価軸と粒度で分解して並べて積んでいくと、正規分布的な図形になることが多い。
体重だったり、足の速さのような身体能力だったり、テストの点数など。
だけども「ものさし」、分解や粒度を間違えると正規分布と呼ぶにはいびつな分布になることがある。

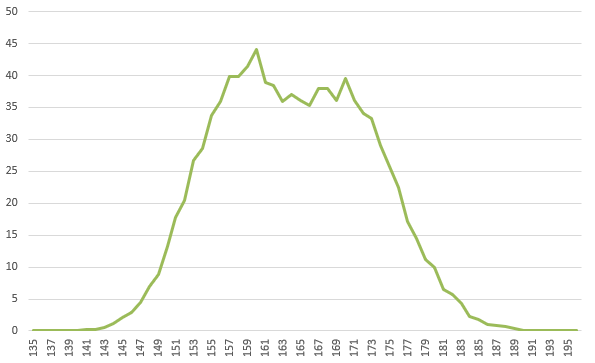
これは平成３１年の高校３年生の身長の分布図。
中央のもりあがりの部分が２つにわかれているように見えるのは、なんのことはない、これが男女をわけていない身長の分布だからだ。

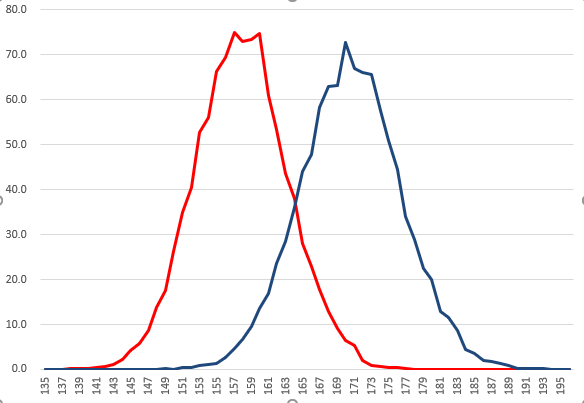
これを男女別々に分布を取ればきれいな正規分布の曲線が２つとれる。お山が２つあるので二項分布と呼ばれたりする。身長は年齢や性別と相関があるので、これを無視して結果を混在させると、要素によってお山が割れたりする。逆に多項分布になったときは、その要因を見極めて分解してやれれば、正規分布を得ることができたりするものだ。（ここでは説明はしないけど算術平均、最頻値、中央値ぐらいは知っておくと、幸せになれるとおもうので、もし知らなければ統計本の一冊でいいから読んで損はない。）（男子の「１６９じゃない１７０だ！」というのが統計からも見えて涙ぐましい。）

だが、世の中そんなにすべてが綺麗に正規分布をとるわけではない。
先の男女ごちゃまぜにした身長の分布のように、要素の分解を間違えると、比較が意味のないデータ群になったりすることもある。赤ん坊や寝たきりの老人まで混ぜた５０ｍ走の結果には、計測不能データが多く混じることだろう。５０ｍ泳法バタフライなんかになれば、さらに計測不能だらけだ。

フルイにかけて粒を同じようなもので並べて、測る、計る、量る。
はかった結果、比較可能な数字にするのは割り算だ。粒度の設定が必要になる。
身長ならセンチというものさしをつかっての割り算で、人間の体重ならキログラムというスケールを用いる。だが金魚の体重ならグラムで、クジラの体重はトンで比較せねばなるまい。コホート、ものさしが一緒だから並べることに意味がでてくるし、並び替えたり、その分布をみて比較、並び替えができる。

分布が集計により統計的にわかっているから、例えば身長ひとつとっても、異常値や外れ値がわかるのであり、それを判断材料として、なにかしらの対応が必要なものを判別することができるわけだ。逆に統計がみえないと、個別のエピソードで悲劇を語ったり、自身が体感した観測範囲でしかものを言えなくなる。リスクとベネフィットの比較はできず、ワクチン反対運動とかコロナなんてただの風邪とかエビデンスなにそれになる。

オリンピックのような競技大会は、大会に参加するのに参加標準記録のようなフィルターを設けたり、格闘技であれば、体重階級別に分けたり、風速などを揃えたりすることで、結果の分布が正規分布に近づくルール設定がなされる。昨今はLGBTQがらみで元男性アスリートが女子大会に出て記録上位を攫って物議を醸したりしていたが、女子の大会結果だけが多項分布になるようなことが続くのであれば競技としては別のルールが制定されるだろう。結果の点数分布が正規分布とは程遠い形になるになるような競技やテストには、環境や作題に問題がある場合がある。

±２σ 以下だと 95.45%がその中におさまり、±３σでは99.73%はその範囲に収まる。
±３σに収まらないのは稀な存在ではあるが、例えばそれが学校の成績のようなものであれば、主席とビリッけつのようなもので、ありはするものだ。

はて、さて、この±３σにも収まらない例外を人間社会はどう扱うのだろうか。
特に日本は標準を尊ぶので、上にも下にも外れるとなかなか厳しい社会ではある。
能力、年収、容姿。上に抜けても下に抜けてもずいぶんと大変そうだ。
政治信条（政治的スペクトル）が右左３σから外れるような主張はもはや見なかったことにされるだろう。
逆にyoutubeやInstagramなんかのSNSは、±３σからはみ出る極端さがないと、注目を集めない。

運動能力や知的指数であればどうか。±３σから外れれば身体障害者や知的障害者として99%の人たちから保護される対象になるかもしれない。逆に、±２σに収まる９５％の人がそうであるようなものを病気として、社会全体が支える社会保障対象にするのは成立しないだろう。（なので、身長無視して腹囲８５ｃｍ以上は一律メタボとか言うのやめよー？）

知能指数も正規分布に近い曲線を描くことになるが、知的障害の場合、知能指数は50～69程度が軽度知的障害者となり障害者となるが、知能指数は70～85程度はボーダー（境界域）は障害者ではないとなる。能力は平滑線をとるが、社会的支援は階級的となる。ここには少し悲劇がある。もっと将来はどうだろうか。経済的に付加価値を生み出せる産業が高度な知的産業ばかりになり、そのボーダーがやがて１００まで引き上げられたら？１２０、１４０・・・と。

加齢により運動機能は低下する。ある程度までいくと介護が必要になる。若者が減り、より老老介護に頼らざるをえない状況になったら？

９９％の人が１％の人を支える、９５％の人が４．５％の人々を扶養する、６８％の人が３２％の人々をフォローする。それとも、０．５％の人が９９．５％の人をひさぐ職をつくることができるのか。はてさて。障害という粒も、やがては、有効数字の彼方に消えゆくものなのかもしれない。

・・・が、過渡期は地獄よな。

参考

学校保健統計調査 / 令和元年度 全国表
www.e-stat.go.jp/stat-search/files?page=1&query=%E8%BA%AB%E9%95%B7%20%E5%88%86%E5%B8%83&layout=dataset&stat_infid=000031925051&metadata=1&data=1

日本人の3分の1は日本語が読めない!?
business.nikkei.com/atcl/NBD/19/special/00261/

正規分布
ja.wikipedia.org/wiki/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83

知的障害
ja.wikipedia.org/wiki/%E7%9F%A5%E7%9A%84%E9%9A%9C%E5%AE%B3